Recent works on Operator Framework for Learning Dyanmical Systems
In this post I will try to give a brief summary of some of the key papers of my most prominent research-line on operator-based data-driven modelling techniques for dynamical systems accomplished during the past two years at Computational Statistics and Machine Learning (CSML) group of the Italian Institute of Technology (IIT). The seeds were planted during rich, inspiring dialogues I had with Pietro Novelli back at the end of 2021. At that time, both Pietro and I were newbies in machine learning, he coming from physics and I from numerical mathematics. A few months later, we wrote our first work, which marked the beginning of this adventure. Besides the amazing team at IIT led by Massimiliano Pontil, major driving force for these projects also lies in Karim Lounici from École Polytechnique. While I discuss key papers in detail, it is worth noting that successful collaborations with other two IIT groups Dynamic Legged Systems led by Claudio Semini and Atomistic Simulations led by Michele Parrinello, resulted with joint works [P9, P10] and [P7, P11], respectively.
Our approach
This research line stems from the Markov/Transfer operator (TO) approach, which is a powerful framework for data-driven modelling of dynamical systems that enables the study of system evolution by lifting it to a higher-dimensional function space. For continuous-time dynamics, the Infinitesimal generator (IG) provides a more refined tool, capturing instantaneous rates of change. Unlike TOs, which describe system evolution over finite time intervals, the IG as a differential operator directly governs the system’s local behavior. The spectral decomposition of the IG and TOs is crucial for identifying dominant dynamical modes and understanding long-term behavior, particularly in stochastic or complex systems. The main reason to choose this mathematical formalism lies in our objectives to develop reliable, efficient and interpretable learning algorithms that are rooted in the careful combination of cutting-edge tools and methods of machine learning, operator theory, statistics and numerical mathematics.
Key Publications
[P1] Kostic, V. R., Novelli, P., Maurer, A., Ciliberto, C., Rosasco, L., and Pontil, M., Learning dynamical systems via Koopman operator regression in reproducing kernel Hilbert spaces. In NeurIPS 2022
[P2] Kostic, V. R., Lounici, K., Novelli, P., and Pontil, M. (2023). Sharp spectral rates for Koopman operator learning. In NeurIPS2023
[P3] Kostic, V. R., Inzerili, P., Lounici, K., Novelli, P., and Pontil, M. (2024). Consistent Long-Term Forecasting of Ergodic Dynamical Systems. In ICML2024
[P4] Meanti, G., Chatalic, A., Kostic, V., Novelli, P., Pontil, M., and Rosasco, L. (2023). Estimating Koopman operators with sketching to provably learn large scale dynamical systems. In NeurIPS2023
[P5] Kostic, V. R., Novelli, P., Grazzi, R., Lounici, K., and Pontil, M. (2024). Learning invariant representations of time-homogeneous stochastic dynamical systems. In ICLR 2024
[P6] Kostic, V. R., Lounici, K., Halconruy, H., Devergne, T., and Pontil, M. (2024). Learning the Infinitesimal Generator of Stochastic Diffusion Processes. In NeurIPS2024
[P7] Devergne, T., Kostic, V.R., Parrinello, M., and Pontil, M. (2024). From Biased to Unbiased Dynamics: An Infinitesimal Generator Approach. In NeurIPS2024
[P8] Kostic, V. R., Lounici, K., Pacreau, G., Novelli, P., Turri, G., and Pontil, M. (2024). Neural Conditional Probability for Inference. In NeurIPS2024
[P9] Ordoñez-Apraez, D., Kostic, V., Turrisi, G., Novelli, P., Mastalli, C., Semini, C., & Pontil, M. (2024). Dynamics harmonic analysis of robotic systems: Application in data-driven koopman modelling. In L4DC
[P10] Ordoñez-Apraez, D., Turrisi, G., Kostic, V. R., Martin, M., Agudo, A., Moreno-Noguer, F., Pontil, M., Semini, C. and Mastalli, C. (2025) Morphological Symmetries in Robotics. (to appear in The International Journal of Robotics Research)
[P11] Devergne, T., Kostic, V., Pontil, M., & Parrinello, M. (2024). Slow dynamical modes from static averages. (submitted to The Journal of Chemical Physics)
Key Contributions
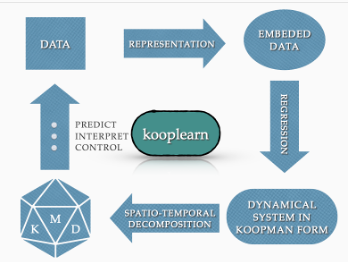
Our initial work [P1] established the first machine learning formulation of the problem of estimating the Koopman/Transfer operators from data, which was, despite of popularity of developed methods for this task, missing in the literature. This led to development of a methodological pipeline for data-driven dynamical systems, depicted in Figure 1, used to create the code-base Kooplearn, which is in continuous development. This foundational step was indeed the beginning of understanding the possibility/impossibility results on learning these operators from finite data samples that inspired other papers that followed, ours as well as from other researchers in the field. 
The second paper [P2] introduces pivotal theoretical guarantees for learning spectral decomposition of transfer operators, a critical component for interpretable modeling of nonlinear dynamical systems. While diverse data-driven algorithms have been available, prior to this work no finite sample guarantees were existing for estimating the key aspect of TO, their spectral decomposition. Our analysis resulted in the development of novel algorithms, notably reduced rank regression (RRR), and introduced the concept of metric distortion to highlight discrepancies between estimated and true eigenfunctions. By developing the theory of sharp spectral learning rates, the paper lays the foundation for more accurate data-driven models, especially when understanding long-term behaviors of dynamical systems.
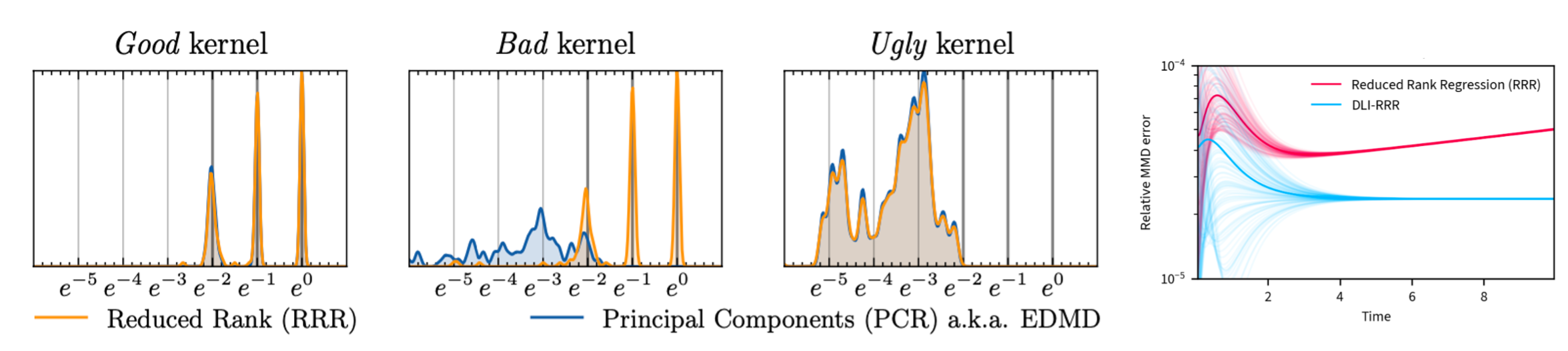
Building upon these insights into spectral estimation, the paper [P3] focuses on addressing one of the key challenges in TO-based methods: long-term reliability in forecasting. While standard operator regression models often fail over extended time horizons due to error explosion or decay, this paper presents the Deflate-Learn-Inflate (DLI) paradigm, which guarantees uniform error bounds even over infinite time scales. Through a combination of eigenvalue deflation and feature centering, we provably stabilize the forecasting process, ensuring that errors remain bounded and consistent for long time horizons. This is particularly relevant in real-world applications where long-term predictions of system states are critical. Our method provides the first non-asymptotic error bounds for infinite horizon forecasting, validated through rigorous numerical experiments, e.g. Figure 2 (right). Together, these two papers contribute to the reliability of AI in scientific domains. By offering the first of their kind theoretical guarantees for both spectral estimation and long-term forecasting, they address the critical issue of ensuring that AI models not only perform well in the short term but also maintain accuracy and stability in the long run. In fields such as climate modeling, epidemiology, and molecular simulations, reliable long-term predictions are essential for informed decision-making.
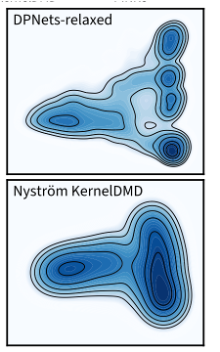
The aspect of efficient learning algorithms for dynamical systems is addressed in works [P4] and [P5]. The former presents a novel method to reduce the computational complexity of kernel-based transfer operator estimation while retaining statistical accuracy by leveraging Nyström sketching. Developed methods allow the computational cost to drop from cubic to almost-linear time complexity while maintaining optimal learning rates. The results are validated through both theoretical error bounds and extensive experiments, particularly on large molecular dynamics datasets, see Figure 2 (below), where the free energy surface of the 2 slowest modes of Chignolin protein folding was estiamted. This contribution is essential for developing scalable AI with provable learning guarantees. In paper [P5] we explored learning the optimal kernel, or in other words, representation learning for dynamical systems. We, introduce Deep Projection Networks (DPNets), which allow one to combine neural networks with operator regression methods to boost the expressivity and robustness, while further reducing the computational complexity, particularly at inference. This approach provably reduces metric distortion and enhance the accuracy of forecasting and spectral decomposition, outperforming traditional methods, see Figure 3 (above).
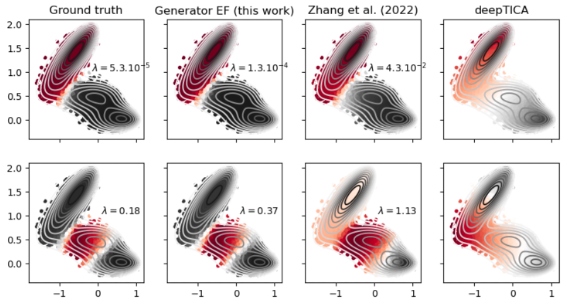
Works [P6] and [P7] specifically focus on the continuous dynamics. The first one establishes a physics-informed framework for learning the infinitesimal generator (IG) of stochastic systems using reproducing kernel Hilbert spaces (RKHS). By incorporating physical priors through energy-based metrics, we provide rigorous statistical learning theory to address the challenge of learning unbounded operators. The former offers learning bounds and ensures robust spectral estimation, making it highly relevant for modeling complex systems like molecular dynamics, where interpretability and adherence to physical laws are of paramount importance. In the latter we introduce a deep learning-based method focused on physics-informed representation learning. The proposed framework addresses crucial aspect of systems that explore their state space slowly, such as molecular systems, making data acquisition very costly or even unfeasible. We show how physics informed IG method can be combined with biased simulations to provably learn the dominant spectral properties of IG, and hence discover modes of slow dynamics (meta-stable states), outperforming traditionally used TO based methods. These results significantly impact the field of atomistic simulations, where slow conformational changes are crucial for understanding molecular dynamics.
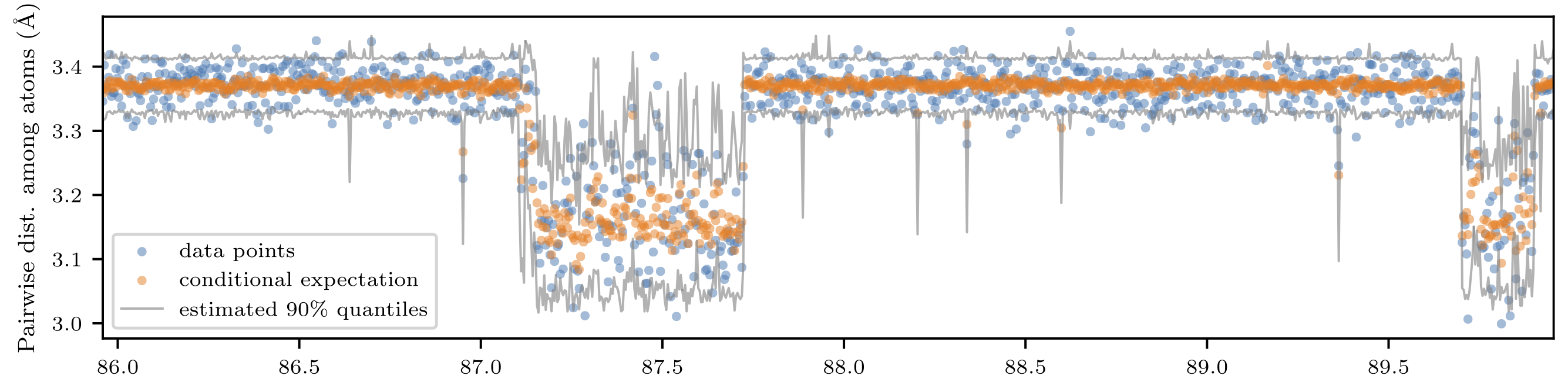
To conclude, the project [P8] introduces Neural Conditional Probability (NCP), a novel operator-theoretic approach for learning conditional distributions. This method is designed to simplify the learning of conditional distributions by using a single, unconditional training phase. The novelty lies in NCP’s ability to construct conditional confidence regions and compute important statistics like conditional quantiles, means, and covariances without the need for retraining, even when conditioning changes. By leveraging neural networks, NCP efficiently handles complex probability distributions, offering both theoretical optimization consistency and statistical guarantees. A primary motivation for this method is to address key challenges in uncertainty quantification (UQ). Current methods, such as non-parametric estimators and conformal prediction, have limitations like inefficiency when the conditioning changes, the curse of dimensionality, or overly conservative confidence intervals. NCP mitigates these issues by offering rigorous theoretical guarantees and an efficient way to compute relevant statistics. Its theoretical non-asymptotic guarantees provide strong assurances about the accuracy and reliability of the model, making it a promising tool for UQ in high-dimensional and nonlinear data settings, see e.g. Figure 5.
Ongoing and future research
Since these two past years have been a great and rewarding research adventure, and the future is definitely full of surprises, my general focus remains on advancing the theoretical and algorithmic aspects of TO/IG-based learning for dynamical systems. Some projcet will be still theoretically driven, where we plan addressing challenges such as learning from partial observations, handling non-time-homogeneous dynamics, and learning spectral decompositions of more general systems (stochastic and deterministic). On the other hand, some of them will be aplication driven, where we plan to use our tools to advance Molecular Dynamics, Neuroscience, Climite Modeling, Robotics and Genetics. Stay tuned!